半導体用語集
ブロッホ振動
英語表記:Bloch oscillation
結晶などの周期構造中に電子を置くとバンド構造が形成され、電子の運動量kを直流電界により増加させていった時に、エネルギー値は真空中の電子のように単純に増大するのでなく、周期的に振動する。したがって、このような構造中の電子に直流電界を加えると、電子は空間的に振動することになり、振動に伴う高周波を取り出せる可能性がある。この周期構造中で期待される電子の振動をブロッホ振動という。普通の結晶では構造周期が小さく、実際にこのような現象が生じるエネルギーはきわめて大きくなる。したがって、実際には電子が加速される途中でフォノン散乱などが生じ、この現象は観測されない(「飽和速度」の項参照)。一方、人工周期構造である半導体超格子を用いると構造周期は大きくなり、実際に到達できるエネルギーでこの現象が生じる。電子が散乱される確率はランダムなので、直流電界下では多くの電子の振動は同期せず、振動を信号として外部に取り出すことは難しいが、電子の減速による((式1)により、E(エネルギー)がkに対して振動する場合、kが大きくなるとm*(有効質量)が負になることによる)負性抵抗が観測される。なお、微小ジョセフソン接合に関しても類似の議論が成立し、振動が観測されている。
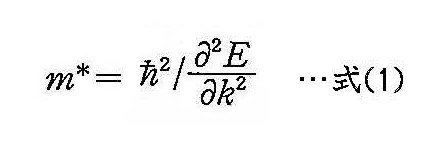
関連製品
「ブロッホ振動」に関連する製品が存在しません。キーワード検索
フリーワードやカテゴリーを指定して検索できます
関連用語
関連特集
「ブロッホ振動」に関連する特集が存在しません。
会員登録すると会員限定の特集コンテンツにもアクセスできます。




