半導体用語集
アレニウスプロット
英語表記:Arrhenius plot
Arrheniusが提唱した反応速度論の式に準じて,寿命の温度依存性をグラフィックに解析する方法。
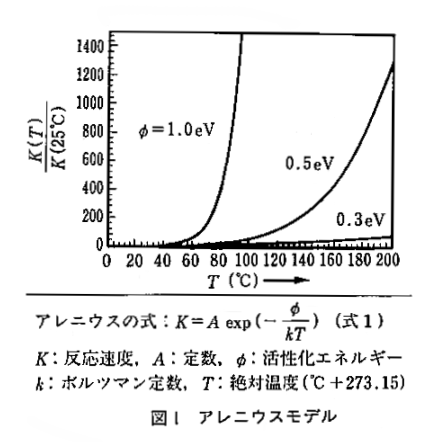
故障時間の温度依存性は,その故障の基になる化学反応の温度依存性に依存する。化学反応の温度依存性は古くからアレニウスの式として知られている。これは図1下部の式1に示すように,反応速度Kと絶対温度T(K)の関係を表わしたものである([K]=[℃]+273.15)⋆。ここで,Aは定数,kはボルツマン定数((1.16×l0⁴)⁻¹eV/K),φは活性化エネルギーである。温度の項がexpの中に入っているため,反応速度は図1に示すように,温度上昇とともに急激に上昇する。図1には,活性化エネルギーの典型的な値である0.3,0.5,1.0eVについて示したが,たとえば,0.5eVの場合には25℃を基準にして100℃では約50倍,200℃では約1,300倍にも上昇する。
故障の多くは化学反応が原因で起きる。そのような故障の寿命時間と化学反応速度との間に逆比例の関係がなりたつと近似すると,寿命(L)は図2下部の式1のようになる。この両辺の対数を取ると式2のようになり,In Lを縦軸(y軸)にとり1/Tを横軸(x軸)に取ると,傾きがφ/kの直線となる。このような構成のグラフ用紙にデータをプロットし,そのデータ点列に当てはまる直線を目の子(目分量)または最小2乗法で引くと,その直線から活性化エネルギーおよび定数が求まる。
具体的にアレニウスプロットで活性エネルギーを求めてみる。半導体デバイスのTEGを試験して対数正規確率紙で解析した結果,150℃で175時間,125℃で1000時間,100℃で7,000時間のメディアン寿命(t₅₀)がえられとする。形状パラメータ(σ)はどの温度でも0.5で変わらなかったとする。アレニウスプロットをするためには,y軸が対数尺,x軸が普通尺のグラフ用紙を用意する。x軸に1/T,y軸にt₅₀を割り当てデータを打点し,目の子で直線を引き,傾きからφ=1.0eVがえられる(図2)。σが温度により変わらなかったと書いたが,これは重要なことである。すなわち上のような解析が意味をなすためには打点する各点の温度で故障のメカニズムおよびモードが不変である必要がある。Lの値としてはメディアン寿命や平均寿命が用いられる。
上で,寿命が反応速度に逆比例すると近似したが,この近似はかなりよい近似である場合も多いが,あくまでも近似であり必ずしもなりたっているとは限らない。
⋆ 習慣上,反応速度を表わす記号として,絶対温度の単位記号と同じKを使っている。混同しないよう注意されたい。
関連製品
「アレニウスプロット」に関連する製品が存在しません。キーワード検索
フリーワードやカテゴリーを指定して検索できます
関連用語
関連特集
「アレニウスプロット」に関連する特集が存在しません。
会員登録すると会員限定の特集コンテンツにもアクセスできます。




